微生物细胞中进行的所有生物化学反应,均服从热力学的基本规律。典型的热力学可定义为在封闭系统中的平衡统计学。相反,活细胞是一开放的、永不平衡的系统;重要的是生命的进程是不可逆的;平衡的反应是不能调节的。
那么,能否应用热力学来了解活细胞的原理?实际上,通过引入“不平衡”或“不可逆”热力学可以克服其中若干限制。Westerfoff等曾成功地分析一些远离平衡的生化系统,包括进出物料流系统。
任何系统的能量变化都属于热力学的范畴。热力学的主要任务是阐明系统从一种状态转变为另一种状态的能量变化。
能量的变化可用各种方式表示,但最有用的是自由能的变化,它提供了一种在常温和常压下预测反应的可行性和反应方向的有效方法。研究能量交换和传递机制离不开热力学的三条基本定律。
热力学第一定律和热焓
每一分子或系统均具有一内在的能(E),此值只取决于其当时的状态。通过在其周围的热的得失或与环境进行功的交换会改变系统的状态。
热力学的第一定律是能量守恒的原理:在任何过程中系统加上其周围的总能量保持恒定,即自然界的总能量守恒。就是能量不能创造出来,也不能消灭,只能从一种形式转化为另一种形式。
若给予一系统一定的热量(Q),必然表现在系统内在能量的变化(ΔE)和系统对环境所做的功(W)。
Q=ΔE+W (2-1)
式中,ΔE=E(产物)-E(反应物)。系统吸收或释放的热量(Q)等于系统内能的变化( ΔE)加上系统对环境所做的功(W)。换句话说,系统获得的总能量要么用来增加其内能,要么用来做功,或者两者都有。
但热量的输入,往往会使系统的体积发生变化(ΔV),而压力(p)保持不变,这意味着对环境做了功:
Q=ΔE+pΔV+W′或Q-W′=ΔE+pΔV (2-2)
因生化反应一般在大气压下,而不在恒体积下进行,这里引进一种热力学参数ΔH(热函量变化又称热焓)来表示热的交换:
ΔHP=Q-W′或ΔHP=ΔEP+pΔV (2-3)
在化学反应中,焓变(ΔH)表示在恒压条件下,系统从反应物到产物的能量变化。这个变化可以是系统吸收或释放的热量,也可以是系统对外做的功。
在恒压下ΔHP是系统吸收的热,可用量热器测量。但量热器是一种恒体积的装置,只能测出ΔEP值。须设法将式(2-3)的最后一项计算出来。已知任何温度下pΔV=nRT。式中n为分子数目,R为气体常数[8.314(J/mol)/K]。由此可得:
ΔHP=ΔEP+nRT (2-4)
这说明每一种化学反应完成后所产生的热和参与反应的分子数量存在定量的关系。
例如,葡萄糖燃烧所发出的热会使量热器的夹层升温,升高多少取决于夹层水量和燃烧的葡萄糖物质的量。这里“燃烧”是指葡萄糖在氧气的作用下发生的氧化反应。这个过程与我们通常理解的燃烧相似,即葡萄糖与氧气反应,产生二氧化碳和水,同时释放出能量。
用此法测得ΔEP=-2815.8kJ/mol葡萄糖(式中负号表示放能反应)。
热的产生是由于复杂有机分子具有一能量高的构型,当把它降解为简单稳定产物,如CO₂和水时,热便释放出来。
若发酵过程的目的是为了获得微生物细胞,就要选择那些完全被微生物利用的养分。因养分的完全利用可获得最大限度的热焓或能,生物可利用这种能来合成细胞和驱动各种需能活动。
微生物利用养分进行生长的这类自发的物理或化学变化所具有的方向性是热力学第一定律所不能解释的。要预测这种反应是否会自发进行或何时进行,还需借助于热力学第二定律和第三定律。
热力学第二定律、第三定律和熵
第二定律阐明自然界中熵的总量是增加的。它指出,在任何自然过程中,一个孤立系统的总熵(代表系统无序程度的物理量)不会减少,通常只会增加。
第三定律指出在绝对零度下所有物质的熵为零。这里的熵为零是当系统的温度趋近于绝对零度时,系统的熵趋近于一个最小值,这个最小值被定义为零。
向一机械提供热能Q,会使系统温度由T1变成T2(T1>T2),则机械所做的功(W)为:

(2-5)
从式(2-5)可见,在任一温度下,成为无效能的那一项必然取决于T2与Q/T1的乘积。Q/T1就是这个体系的熵,常用S表示。故S是一体系的全部能量中所不能做有效功的度量。熵也代表一个系统的紊乱程度。
实际上,任一化学体系在温度T下工作时也服从式(2-6):
G=H-TS (2-6)
式中,G是体系的自由能,即做出有效功的那一部分能量;H是体系中的全部热能(热焓)。
除T外,无法测量这些变量的绝对值。但当体系从原有状态改变为另一状态时,可用G′=H′-S′表示,这样变化前后之差便可用式(2-7)表达:
ΔG=ΔH-TΔS (2-7)
式(2-7)指出,一体系在恒温恒压下从一状态变为另一状态必然伴随自由能的变化。因ΔG是一体系所能做的功的度量,由它决定反应有无可能进行。
因自由能值高,反应体系潜在不稳定,在适合条件下便有可能自发地向自由能低的方向变化。故从不稳定的高化学能化合物变为较稳定的低化学能化合物时必然会释放能,这在热力学上是可行的。
Akinterinwa等将用于产能的分解代谢过程称为燃烧(加燃料)过程。此反应过程主要将源自基质的能量转换成更容易被生物利用的、用于驱动组成代谢的生物能。
此能量的得率取决于被降解的基质,且可用Gibbs自由能的变化ΔG来量化此转换过程:
ΔG=G产物-G反应物 (2-8)
对化学反应的G的估算可运用基质的标准Gibbs自由能(G′0)进行。G′0是定义在T=298K(25℃)和pH=7,初始基质浓度为1mol/L的标准条件下测定。反应的G′0与实际G的关系为:
ΔG=ΔG′0+RTlnQ (2-9)
式中,Q是质量作用比率,定义为产物活性与反应物活性之比,在稀溶液的情况下常用产物浓度与反应物浓度之比估算;R是气体常数[=8.314(J/mol)/K];T是热力学温度,K。
若反应处于平衡状态,ΔG=0,则:
ΔG′0=RTlnKeq (2-10)
式中,Keq是平衡常数。
分解代谢过程的特征是高能基团的转移反应,这是基质分解时释放出的能量通过此反应以生物高能化合物的形式保存。这些高能基团的转移方式是通过磷酸化、酰基、合或氧化还原(redox)反应进行的。
磷酸化反应是用于启动分解过程,因其生成的基质衍生物不会扩散到细胞外,同时将基质保留在胞内也无需花费能量。将基质磷酸化可以使其活性提高,更容易被代谢。典型的例子是糖酵解的起步,葡萄糖被磷酸化成6-磷酸葡萄糖,其反应如下:
①非自发的/吸能的半反应:

(2-11)
②自发的/放能的半反应:
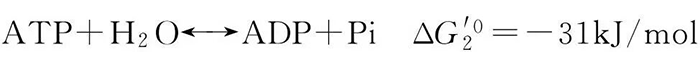
(2-12)
式中,Pi是无机磷酸盐,其总的反应为:

(2-13)
从分解代谢释放出来的能量被有效地通过氧化还原反应与磷酸化反应保存于一些高能化合物的化学键上,如烟酰胺腺苷二核苷酸(NADH)、磷酸烟酰胺腺苷二核苷酸(NADPH)与腺苷三磷酸。
在糖酵解的能量释放步骤,即3-磷酸甘油醛被转化为3-磷酸甘油酸里此反应是通过基质水平磷酸化供给ATP的典型例子。其总的反应过程如下:
3-磷酸甘油醛+ADP+Pi+NAD←→3-磷酸甘油酸+ATP+NADH+H+ ΔG′0=-12.5kJ/mol
在探索发酵工艺的奥秘中,热力学原理扮演着不可或缺的角色。它不仅为我们揭示了反应的自发性,还指导我们如何通过精细调节条件来提升产量和效率。通过巧妙运用热力学,我们能够确保每一分能量都能被微生物充分利用,从而在生产高质量的发酵产品的同时,也注重过程的可持续性。
简而言之,热力学是发酵工艺研究中的指南针,引领我们走向更高效、更环保的未来。希望这篇文章对您有所启发。


